私は昔塾で数学を教えていました。
今回は、「ビュフォンの針」ということで、前回に引き続き確率論の内容で、とっても面白いです!楽しんで読んでください!
前回は、「モンテカルロ法」で円周率の近似値を求めました。
今回は、「ビュフォンの針」で円周率の近似値を求めていきます!
プログラミングスクールに関しては下の記事で詳しく記述しています。
こちらで紹介しているスクールは、すべて無料期間がある優良なスクールのみで、特徴を明確にし、読者のニーズに絞って丁寧に解説しました。初めての一歩として、無料説明会に参加してみてください。
ビュフォンの針とは
ビュフォンの針とは、18世紀の博物学者である、ジョルジュ=ルイ・ルクレール、コント・ド・ビュフォンが提起した数学上の問題です。
彼は、多数の平行線が描かれている床に針を落とすと、平行線と針が交わる確率は、円周率を使って表現できることを数学的に確立しました。この問題は、積分と幾何学を用いることで解けます。

適当に落とした針が平行線が交わる本数を数えることで確率が求まります。
昔の偉人は、コンピュータを使わずにビュフォンの実験を行っていたらしいです!
その結果がこちら!
| ランキング | 名前 | 年 | 投げた回数 | 導いた円周率 |
|---|---|---|---|---|
| 1位 | ウルフ | 1800年代 | 5000 | 3.1596 |
| 2位 | ラッツァリーニ | 1901 | 3408 | 3.1415929 |
| 3位 | スミス・ダベルディーン | 1855 | 3204 | 3.1553 |
| 4位 | レイナ | 1925 | 2520 | 3.1795 |
| 5位 | フォックス大尉 | 1864 | 1030 | 3.1595 |
すでにかなり良い精度で近似値が得られていますが、今回は、もっと回数を多くするため、文明の利器を用いて10万回までシミュレーションしてきます!
円周率の求め方
理屈を知りたい方は、wikipediaか高校数学の美しい物語を参照してください。
wikipedia は数式で理解したい人向け、高校数学の美しい物語は図も多く用いられているため理解しやすいと思います。
今回の記事で重要なのは、最終的な確率と積分によって求められた等式です。
- 平行線の間隔:d
- 針の長さ:l(エル)
- すべての針の本数:N
- 平行線と交わる針の本数:n
$$\frac{n}{N}=\frac{2l}{πd}(l \leq d)$$
$$\frac{n}{N}=\frac{2l}{πd}(1-\sqrt{1-\frac{d^{2}}{l^{2}}})+1-\frac{2}{π}\arcsin(\frac{d}{l})(l>d)$$
これらの式を「π」について解くと
$$π=\frac{2Nl}{nd}$$
$$π=\frac{2Nl}{d(n-N)}(1-\sqrt{1-\frac{d^{2}}{l^{2}}}-\arcsin(\frac{d}{l}))$$
プログラム作成
コメントでコードの解説をしていきます。
読みやすいコードを記述しているつもりですがわからなければコメントを残してくれると嬉しいです。
関数「Buffon」
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 | def Buffon(): n = 0 # 針と平行線が交わる本数のカウント用 N = int(input("針の本数 n:")) d = int(input("平行線の幅 d:")) l = int(input("針の長さ l:")) # インスタンス生成 root = tk.Tk() # ウィンドウのタイトル設定 root.title("Buffon's needle") # ウィンドウサイズ設定 root.geometry("450x450") # 描画領域 h = 450 w = 450 # キャンバスのエリア設定 canvas = tk.Canvas(root, bg="white", height=h, width=w) # 平行線を描写 for i in range(h // d): # 端点(x1, y1)と(x2, y2)を結ぶ直線を描写 canvas.create_line(0, i * d, w, i * d) # ランダムな針を生成 for i in range(N): x1 = random.uniform(d, w - d) y1 = random.uniform(d, h - d) theta = random.uniform(0, 2 * math.pi) x2 = x1 + l * math.cos(theta) y2 = y1 + l * math.sin(theta) # 平行線と針が交わる時 if (y1 // d) != (y2 // d): n += 1 canvas.create_line(x1, y1, x2, y2, fill = "red") # 交わらない時 else: canvas.create_line(x1, y1, x2, y2) # 最後にバインド。位置合わせ。 canvas.place(x = 0, y = 0) print("π:", calc(n, N, l, d)) root.mainloop() |
関数「calc」
「math.sqrt」で平方根を求めることが出来ます。また、「math.asin」で「arcsin」の結果を返してくれます。
1 2 3 4 5 6 7 | # 記事内で解説した通りの式 def calc(n, N, l, d): if l <= d: return (2 * N * l) / (n * d) else: return (2 * N * l / d * (n - N)) * (1 - math.sqrt(1 - d ** 2 / l ** 2) - math.asin(d / l)) |
メイン関数
関数「Buffon」を呼び出します。
1 2 3 | if __name__ == "__main__": Buffon() |
全体コード
最後にすべてをまとめたコードを載せます。コピペして実行してみると面白いです。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 | import tkinter as tk import random import math def Buffon(): n = 0 N = int(input("針の本数 n:")) d = int(input("平行線の幅 d:")) l = int(input("針の長さ l:")) root = tk.Tk() root.title("Buffon's needle") root.geometry("450x450") h = 450 w = 450 canvas = tk.Canvas(root, bg="white", height=h, width=w) for i in range(h // d): canvas.create_line(0, i * d, w, i * d) for i in range(N): x1 = random.uniform(d, w - d) y1 = random.uniform(d, h - d) theta = random.uniform(0, 2 * math.pi) x2 = x1 + l * math.cos(theta) y2 = y1 + l * math.sin(theta) if (y1 // d) != (y2 // d): n += 1 canvas.create_line(x1, y1, x2, y2, fill = "red") else: canvas.create_line(x1, y1, x2, y2) canvas.place(x = 0, y = 0) print("π:", calc(n, N, l, d)) root.mainloop() def calc(n, N, l, d): if l <= d: return (2 * N * l) / (n * d) else: return (2 * N * l / d * (n - N)) * (1 - math.sqrt(1 - d ** 2 / l ** 2) - math.asin(d / l)) if __name__ == "__main__": Buffon() |
出力結果
ここでは、「d」= 50, 「l」= 25と固定して結果をまとめていきます。
まずは100本!

求まった「π」の近似値は、π: 3.3333333333333335でした。
次に1000本!

求まった「π」の近似値は、π: 3.2467532467532467でした。
先ほどよりも精度が良くなりました!
次に10000本!
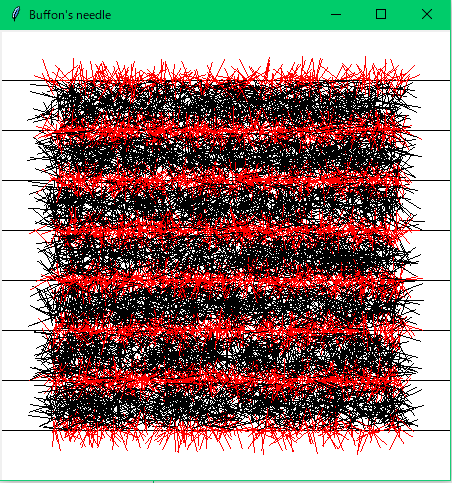
求まった「π」の近似値は 、π: 3.1486146095717884でした。
すごいですね!ほぼ円周率です!
あと、この画面がかわいく見えてきます♡
次に100000本!

求まった「π」の近似値は 、π: 3.14564328405158874でした。
有刺鉄線みたいで面白いですねぇ~!
最後に100万本もやったのですが、僕の低スペックノートPCでは実行できませんでした笑。
ごめんポチ!
まとめ
今回は、ビュフォンの針で円周率の近似値を求めるプログラムを作成してみました。10万本で実行すると針がびっしり敷き詰められて、円周率の近似値が、確率と積分によって求められるのが直感的にわかりますね!
この考え方は、以前、「モンテカルロ法」でも円周率の近似値を求めていますのでもしよろしければそちらもご覧ください。
最後まで記事を読んでいただきありがとうございます!
昔、自分が参考にしていたプログラミングについての書籍を紹介します。
非常にわかりやすい内容で、言語は「Java」ですが参考にしてみてください!
プログラミングスクールに関しては下の記事で詳しく記述しています。
こちらで紹介しているスクールは、すべて無料期間がある優良なスクールのみで、特徴を明確にし、読者のニーズに絞って丁寧に解説しました。初めての一歩として、無料説明会に参加してみてください。
 ナノトイラボ
ナノトイラボ 




