今回は微分法を用いて極値を求める方法と、極値を直接求めることができるSysPyのライブラリの一つであるargrerlmax、argrelminを用いて極大値・極小値を求める方法を解説していきます。
さらに、求めた極値が視覚的にわかるようにグラフに表示する方法も解説しています。
極値を求めて増減表を作成するには、「Pythonで関数の極大・極小値を求めて増減表を書こう!」で詳しく解説していますのでそちらも参考にしてください。
コンテンツ
無料オンライン相談を活用しよう!
Pythonというプログラミング言語は機械学習の人気の高まりなどもあり、様々なスクールが無料説明会を開催しています。
その中でも「Freeks(フリークス)|業界初!10,780円のサブスク型プログラミングスクール」がオススメです。Pythonを効率よく学びたいという方はまずは適性を知るためにも無料説明会を利用しましょう。
微分法の利用
今回はすべてのプログラムにおいて下記の式の極値を求めます。
$$f(x)=x^{3} – 3x$$
極値を求める
極値を求める方法は以下の2つの方法があります。
- 微分法によって求める
- 関数から直接極値のインデックスを取得する
順番に解説していきます!
まずは、関数f(x)を微分し、f'(x)=0となるxを求める方法です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
import sympy as sym # "x"を変数とする x = sym.Symbol("x") # 関数を決定 expr = x**3 - 3*x print("f(x) = {}".format(expr)) # "x"で微分する diff = sym.diff(expr, x) print("f'(x) = {}\n".format(diff)) # f(x) = 0を解く。極値が求まる critical_points = sym.solve(diff) # すべての極値に対する処理 for critical_point in critical_points: # 微分した関数の"x"に「critical_point」を代入。この値は当然0 f_dash_x = diff.subs(x, critical_point) # 微分前の関数の"x"に「critical_point」を代入。f(critical_point) f_x = expr.subs(x, critical_point) print("x = {}のとき:f'(x) = {}, f(x) = {}".format(critical_point, f_dash_x, f_x)) """ f(x) = x**3 - 3*x f'(x) = 3*x**2 - 3 x = -1のとき:f'(x) = 0, f(x) = 2 x = 1のとき:f'(x) = 0, f(x) = -2 """ |
ただし、このままのプログラムだと極値は求められていますが、極大値なのか極小値なのかが判断できません。
そこで、2階微分を行うことで、極大値・極小値の判断をしていきます。
2階微分によって極大値・極小値を求める
数学的に求めるならば、2階微分した関数に対して、ある極値を代入した値が正ならば極小値、負ならば極大値と判断することができます。
関数f(x)に対して1階微分をf'(x)、2階微分したものをf”(x)とします。
- f'(x)=0となる極値x=aにおいて、f”(a)<0のとき
→ f(x)はx=aで極大値f(a)をとる - f'(x)=0となる極値x=aにおいて、f”(a)>0のとき
→ f(x)はx=aで極小値f(a)をとる
ちなみに、f”(a)=0かつ、その前後で符号が切り替わるとき、点(a, f(a))を変曲点といいます!
単純に極値を求めるときとの違いは、2階微分を行う処理が追加されるのと、極大値か極小値を判断するための条件式が追加されています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
import sympy as sym # "x"を変数とする x = sym.Symbol("x") # 関数を決定 expr = x**3 - 3*x print("f(x) = {}".format(expr)) # "x"で微分する diff_1 = sym.diff(expr, x) print("f'(x) = {}".format(diff_1)) # "x"で微分する(2階微分) diff_2 = sym.diff(diff_1, x) print("f''(x) = {}\n".format(diff_2)) # f'(x) = 0を解く。極値が求まる critical_points = sym.solve(diff_1) # すべての極値に対する処理 for critical_point in critical_points: # f(critical_point)を求める f_x = expr.subs(x, critical_point) # f''(critical_point)を求める。(これは加速度に相当) alpha = diff_2.subs(x, critical_point) # 加速度が負の時 if alpha < 0: print("x = {}のとき:極大値{}をとる".format(critical_point, f_x)) elif alpha > 0: print("x = {}のとき:極小値{}をとる".format(critical_point, f_x)) """ f(x) = x**3 - 3*x f'(x) = 3*x**2 - 3 f''(x) = 6*x x = -1のとき:極大値2をとる x = 1のとき:極小値-2をとる """ |
SysPy・argrelmax・argrelminの利用
これまでは、数学的な考え方で極大値・極小値を求めてきましたが、「SysPy」のライブラリの中には「argrelmax」「argrelmin」という関数が存在し、一発でそれらの値をもとめることができます!
とっても便利ですが、「極値」ではなく極値のインデックスが取得できる点に注意してください!
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
import numpy as np from scipy import signal import matplotlib.pyplot as plt # 求める関数を設定 func = lambda x : x ** 3 - 3 * x # x, y座標に対応する点を決定。0.01ずつのループ x = np.arange(-5, 5, 0.01) # x座標に対応するyの値を取得 y = np.array([func(i) for i in x]) # 極大値・極小値をとるインデックス(x座標)を取得 maxid = signal.argrelmax(y) minid = signal.argrelmin(y) print(x[maxid], y[maxid]) print(x[minid], y[minid]) print("x = {}のとき:極大値{}をとる".format(x[maxid][0], y[maxid][0])) print("x = {}のとき:極小値{}をとる".format(x[minid][0], y[minid][0])) """ [-1.] [2.] [1.] [-2.] x = -1.0のとき:極大値2.0をとる x = 1.0のとき:極小値-2.0をとる """ |
ここでは、極値を調べる関数を「lambda」という無名関数を用いて記述しました。こちらについての解説は別記事を読むとわかりやすいと思います。
また、関数を調べる粒度は0.01ずつとするため、「numpy.arange」を用います。こちらの使い方も別記事ではありますが、「Pythonで0.1刻みにfor文のループをする方法」を参考にしてください。
グラフ表示
最後に、極値がどこにあるのかを視覚的にわかりやすいよう、グラフに表示していきます!
ソースコード
18行目以降がグラフを描くコードです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
import numpy as np from scipy import signal import matplotlib.pyplot as plt # 求める関数を設定 func = lambda x : x ** 3 - 3 * x # x, y座標に対応する点を決定。0.01ずつのループ x = np.arange(-5, 5, 0.01) # x座標に対応するyの値を取得 y = np.array([func(i) for i in x]) # 極大値・極小値をとるインデックス(x座標)を取得 maxid = signal.argrelmax(y) minid = signal.argrelmin(y) plt.plot(x, y) # 補助線の追加 plt.grid() # 極大値・極小値を「〇」で表示(アルファベットのオー) plt.plot(x[maxid[0]], y[maxid[0]], "o") plt.plot(x[minid[0]], y[minid[0]], "o") plt.show() |
出力結果
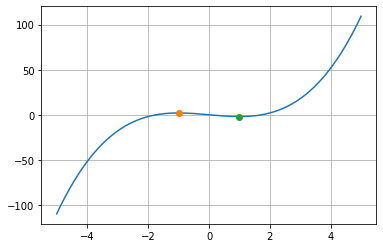
ちなみに、複数の極大値・極小値が存在してもすべて表示されます!
是非関数を変えて実行してみてください!
まとめ
今回は、微分法を用いた方法や、SysPyのライブラリである、argrelmax、argrelminを用いて極値を求める方法を記述しました。
少しでも参考になれば幸いです。
極値を求めて増減表を作成するには、「Pythonで関数の極大・極小値を求めて増減表を書こう!」で詳しく解説していますのでそちらも参考にしてください。
無料の説明会を有効活用しよう!
独学での学習は孤独感を感じやすく挫折してしまう初心者も多いです。また、参考書を購入しても全く読む気にならないという方も多いはずです。
それでも、なんとかPythonの勉強を行い、高スキルなエンジニアを目指したいという方は無料で受けられるオンライン説明会に参加してみることも一つの手です。
Pythonというプログラミング言語は機械学習の人気の高まりなどもあり、様々なスクールが無料説明会を開催しています。
その中でも「Freeks(フリークス)|業界初!10,780円のサブスク型プログラミングスクール」がオススメです。Pythonを効率よく学びたいという方はまずは適性を知るためにも無料説明会を利用しましょう。
パソコン操作にお困りではありませんか?
ExcelやWordなど、基本的なソフトの使い方がいまいちわからないという方には、「PCHack」という講座をオススメしています。スクールの中でもコストパフォーマンスに優れ、オンラインなのでどこでも好きな時間に学習できます。
3万円ほどでPC初心者を脱出したい方は参考にしてください。
【PC初心者必見!】パソコンの勉強方法が分からないならPCHack講座がオススメ!

 ナノトイラボ
ナノトイラボ 


