今回は、Pythonを用いてモンテカルロ法によって円周率を求め、精度評価のシミュレーションをしていきます!楽しんで読んでください!
今回のコードの参考になると思われる記事をまとめておきます。
参考:【Python入門】初めてのプログラミング(ラムダ式 : 無名関数, lambda)
参考:【Python入門】初めてのプログラミング(スコープと関数)
参考:年金の最適受給月はいつか?Pythonでシミュレーション
プログラミングスクールに関しては下の記事で詳しく記述しています。
こちらで紹介しているスクールは、すべて無料期間がある優良なスクールのみで、特徴を明確にし、読者のニーズに絞って丁寧に解説しました。初めての一歩として、無料説明会に参加してみてください。
モンテカルロ法とは
モンテカルロ法とは、乱数を用いて、シミュレーションや数値処理を行う手法です。
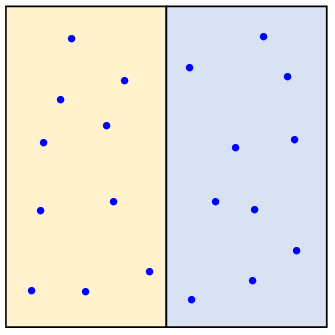
下の図を見てください。青い点は、乱数を用いて打った点だと考えてください。青い点を数えると、(左:右)=(10:10)=(1:1)になります。なので、面積比も1:1になります。
今回は、説明のため点の数は20個ですが、この点の数が10万以上あれば、より正確な値が得られ、誤差は0.1%以内になるといわれています。
円周率の求め方
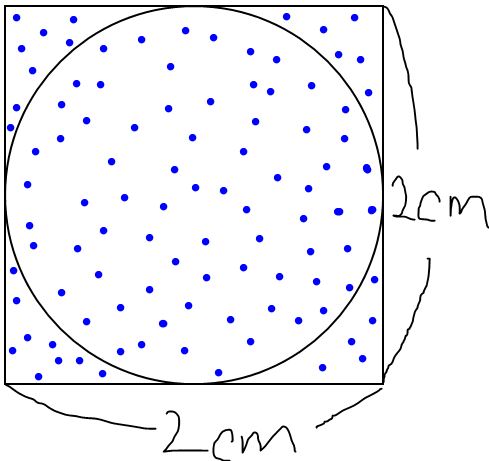
今回は、円周率である、「π」の近似値を求めます。次のような条件の元考えていきます。
- 正方形の1辺の長さを2cmとすると、内接する円の半径は1cmとなる。
- 青い点の総数をNとする。
- 円の中にある青い点の数をnとする。
これらの条件と、面積比、円の面積を求める公式から、
2 × 2 : 1 × 1 × π = N : n
よって、
π = 4n / N
となります。簡単ですね!
モンテカルロ法シミュレーション
ここからはPythonを用いてモンテカルロ法のシミュレーションを行っていきます。
プログラムの作成
単純に円周率を求めるだけなら以下のコードでできます。
何をしているのかが理解できれば大丈夫です。
円の原点を(0, 0)としています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
import random import math def Monte_Carlo(): # 原点と任意の点までの距離を求める関数 distance = lambda x, y : math.sqrt(x ** 2 + y ** 2) # 試行回数の設定 N = int(input("試行回数")) # 円の中にあることを判定する変数 R = 1 # 円の中にある点を数える変数 n = 0 for _ in range(N): # -1 ~ 1までのランダムな浮動小数点(float型) x = random.uniform(-1, 1) y = random.uniform(-1, 1) r = distance(x, y) if r <= R: n += 1 print(4 * n / N) if __name__ == "__main__": Monte_Carlo() """ 試行回数1000 3.216 """ |
ただ、これだけだとつまらないのでコードを書き換えて視覚的にみていきましょう!
ラムダについては次の記事を参考にしてください。
参考:【Python入門】初めてのプログラミング(ラムダ式 : 無名関数, lambda)
10万回の視覚的試行
次は、どのように点が取られているのかを視覚的にわかるようにグラフ描写していきます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 |
import matplotlib.pyplot as plt import numpy as np import random import math def Monte_Carlo(): distance = lambda x, y : math.sqrt(x ** 2 + y ** 2) # 試行回数 N = 100000 # グラフ描写用配列 x_list = np.zeros(N) y_list = np.zeros(N) R = 1 n = 0 for i in range(N): x = random.uniform(-1, 1) x_list[i] = x y = random.uniform(-1, 1) y_list[i] = y r = distance(x, y) if r <= R: n += 1 print("π :", 4 * n / N) print("内側の点 :", n, "個") print("外側の点 :", N - n, "個") draw_graph(x_list, y_list) def draw_graph(x_list, y_list): c1 = plt.Circle((0, 0), radius=1, fc="None", ec="r", linewidth=2) ax = plt.gca() ax.add_patch(c1) plt.axis("scaled") plt.xlim(-1, 1) plt.ylim(-1, 1) plt.xlabel("X") plt.ylabel("Y") plt.scatter(x_list, y_list, marker=".", color = "blue", label = "POINT") plt.show() if __name__ == "__main__": Monte_Carlo() """ π : 3.14472 内側の点 : 78618 個 外側の点 : 21382 個 """ |


上の画像は、青い点が、ランダムに打たれたものです。点が重なり合って、右側の画像は、もはや肉眼では背景のように見えます。これだけ多くの点を打てれば、感覚的にも、点の数の比がそのまま面積比と近似値をとることはわかりますね!
実際、出力例では、円周率π = 3.14472 となっており、求める結果に近いことが確認できました!すごいですね!
まとめ
最後までお読みいただきありがとうございます。
今回は、乱数を用いて数値処理を行う、「モンテカルロ法」をPythonを用いて実装してみました。乱数で円周率が求まる理屈がご理解いただけましたでしょうか?
モンテカルロ法で調べてみると、4分の1の円で考えている記事が多かったのですが、普通の円で考えることで理解しやすいと思い自分なりに書いてみました。
10万回という人間の手ではほぼ不可能なことでも、コンピュータの力を使えばこんなに簡単にシミュレーションができるすごさや面白さ、数学的な考え方をこれからも伝えていきたいと思います。
プログラミングスクールに関しては下の記事で詳しく記述しています。
こちらで紹介しているスクールは、すべて無料期間がある優良なスクールのみで、特徴を明確にし、読者のニーズに絞って丁寧に解説しました。初めての一歩として、無料説明会に参加してみてください。
パソコン操作にお困りではありませんか?
ExcelやWordなど、基本的なソフトの使い方がいまいちわからないという方には、「PCHack」という講座をオススメしています。スクールの中でもコストパフォーマンスに優れ、オンラインなのでどこでも好きな時間に学習できます。
3万円ほどでPC初心者を脱出したい方は参考にしてください。
【PC初心者必見!】パソコンの勉強方法が分からないならPCHack講座がオススメ!

 ナノトイラボ
ナノトイラボ 



