今回は、Pythonで、高校数学で扱う増減「表」を作っていきます。
数学の微分積分を解いていて、「いい加減増減表書くのだりぃ」って方は、PCに解いてもらいましょう~笑
増減表をPythonで書いている記事を調べても出てこなかったので僕がパイオニアです♡
極値求める方法を詳しく知りたい方は「Pythonで極値(極大値・極小値)を求める方法【SysPy・argrelmax・argrelmin】」を参考にしてください。
また、関数を描画するほう方法については下の記事を参考にしてください。
コンテンツ
無料オンライン相談を活用しよう!
Pythonというプログラミング言語は機械学習の人気の高まりなどもあり、様々なスクールが無料説明会を開催しています。
その中でも「Freeks(フリークス)|業界初!10,780円のサブスク型プログラミングスクール」がオススメです。Pythonを効率よく学びたいという方はまずは適性を知るためにも無料説明会を利用しましょう。
この記事の目的と最終結果
目的は、増減表を作成することです。
$$x^{4} – 4x^{2} + 1$$
このような数式をプログラムに入力すると、自動的に以下のようなグラフと表が出力されます。

1 2 3 4 5 6 7 8 | ------------------------------------------------------------------------------------------------------------------------------------------------------- | x || -sqrt(2) - 1 | ・・・ | -sqrt(2) | ・・・ | 0 | ・・・ | sqrt(2) | ・・・ | 1 + sqrt(2) | ------------------------------------------------------------------------------------------------------------------------------------------------------- | f'(x) || | - | 0 | + | 0 | - | 0 | + | 0 | ------------------------------------------------------------------------------------------------------------------------------------------------------- | f(x) || -4*(-sqrt(2) - 1)**2 + 1 + (-sqrt(2) - 1)**4 | ↘ | -3 | ↗ | 1 | ↘ | -3 | ↗ | -4*(1 + sqrt(2))**2 + 1 + (1 + sqrt(2))**4 | ------------------------------------------------------------------------------------------------------------------------------------------------------- |
上の画像では、出力結果の表の体裁が整えているのですが、環境依存文字のせいか、ツールのせいなのかはわかりませんが、下のように、文字として表現すると、表の位置ずれが出てしまいます。
プログラムを実行した際には、ちゃんと表の体裁は整っているので、ぜひとも「google colaboratory」などで確認してみてください。
極大値・極小値とは
極大値・極小値とは微分法における極値と呼ばれるものです。
関数f(x)に対しての微分をf ‘(x)とします。
- f ‘(x)の値がx = aの前後で、正から負に変化するとき
→ f(x)はx = aで極大値f(a)をとる - f ‘(x)の値がx = aの前後で、負から正に変化するとき
→ f(x)はx = aで極小値f(a)をとる - 極大値・極小値をまとめて極値という
ここは大丈夫だね!
微分した関数は、f(x)の傾きを示すよ!
増減表とは
増減表とは、関数の概形を調べる為のもので、極値をまとめた表のことです。
具体的には、以下のような項目で表が完成します。
$$f(x) = x^{3} – 4x^{2} + 1$$
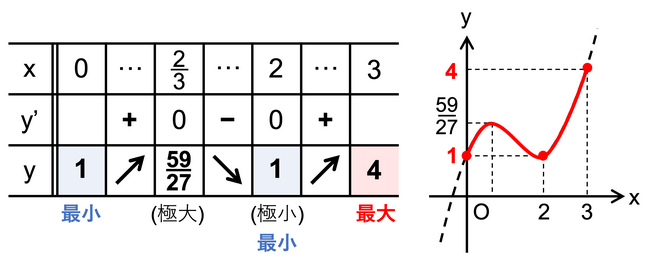
増減表の書き方
関数の描画と極値を求める
$$f(x) = x^{3} – 4x^{2} + 1$$
上の関数について調べていきます。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 | # グラフを描画する関数 def make_graph(): # 表で出力する値のリスト。極値と、定義域での値の保存用 data = [] # "x"を変数と設定 x = sym.Symbol("x") # 関数の設定 expr = x**3 - 4*x**2 + 4*x + 1 print("f(x) = {}".format(expr)) # "x"で微分 diff = sym.diff(expr, x) print("f'(x) = {}".format(diff)) # f'(x) = 0を解く。極値を求める critical_points = sym.solve(diff) for critical_point in critical_points: # 極値でのf'(x)を求める。この値は当然0になる f_dash_x = diff.subs(x, critical_point) # 極値でのf(x)を求める f_x = expr.subs(x, critical_point) print("x = {}のとき:f'(x) = {}, f(x) = {}".format(critical_point, f_dash_x, f_x)) data.append((critical_point, f_x)) # 極値のx座標でソート data = sorted(data) # 定義域を(極値のx座標の最小値 - 1 <= x <= 極値のx座標の最大値 + 1)とする plot(expr, (x, data[0][0] - 1, data[-1][0] + 1)) data.insert(0, (data[0][0] - 1, expr.subs(x, data[0][0] - 1))) data.append((data[-1][0] + 1, expr.subs(x, data[-1][0] + 1))) return data |
増減表の作成
ここでは、表の体裁を整えるために試行錯誤しました。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 | # 増減表を作成する関数 def make_table(data): symbol = lambda a, b : (" + | ", " ↗ | ") if a < b else (" - | ", " ↘ | ") x, f_dash_x, f_x = "| x || ", "| f'(x) || ", "| f(x) || " for i, d in enumerate(data): s, t = d[0], d[1] space = max(len(str(s)), len(str(t))) if i == 0: x += str(s) + " " * (space - len(str(s))) + " | " f_dash_x += " " * space + " | " f_x += str(t) + " | " else: symbols = symbol(t_odd, t) x += "・・・ | " + str(s) + " " * (space - len(str(s))) + " | " f_dash_x += symbols[0] + "0" + " " * space + "| " f_x += symbols[1] + str(t) + " " * (space - len(str(t))) + " | " t_odd = t max_len = max(len(x), len(f_dash_x), len(f_x)) - 1 print("-" * max_len) print(x) print("-" * max_len) print(f_dash_x) print("-" * max_len) print(f_x) print("-" * max_len) |
メイン関数
作成した関数を呼び出していきます。
1 2 3 4 5 6 7 8 | import sympy as sym from sympy.plotting import plot if __name__ == "__main__": data = make_graph() make_table(data) |
全体のコード
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 | import sympy as sym from sympy.plotting import plot def make_graph(): data = [] x = sym.Symbol("x") expr = x**3 - 4*x**2 + 4*x + 1 print("f(x) = {}".format(expr)) diff = sym.diff(expr, x) print("f'(x) = {}".format(diff)) critical_points = sym.solve(diff) for critical_point in critical_points: f_dash_x = diff.subs(x, critical_point) f_x = expr.subs(x, critical_point) print("x = {}のとき:f'(x) = {}, f(x) = {}".format(critical_point, f_dash_x, f_x)) data.append((critical_point, f_x)) data = sorted(data) plot(expr, (x, data[0][0] - 1, data[-1][0] + 1)) data.insert(0, (data[0][0] - 1, expr.subs(x, data[0][0] - 1))) data.append((data[-1][0] + 1, expr.subs(x, data[-1][0] + 1))) return data def make_table(data): symbol = lambda a, b : (" + | ", " ↗ | ") if a < b else (" - | ", " ↘ | ") x, f_dash_x, f_x = "| x || ", "| f'(x) || ", "| f(x) || " for i, d in enumerate(data): s, t = d[0], d[1] space = max(len(str(s)), len(str(t))) if i == 0: x += str(s) + " " * (space - len(str(s))) + " | " f_dash_x += " " * space + " | " f_x += str(t) + " | " else: symbols = symbol(t_odd, t) x += "・・・ | " + str(s) + " " * (space - len(str(s))) + " | " f_dash_x += symbols[0] + "0" + " " * space + "| " f_x += symbols[1] + str(t) + " " * (space - len(str(t))) + " | " t_odd = t max_len = max(len(x), len(f_dash_x), len(f_x)) - 1 print("-" * max_len) print(x) print("-" * max_len) print(f_dash_x) print("-" * max_len) print(f_x) print("-" * max_len) if __name__ == "__main__": data = make_graph() make_table(data) |
出力結果
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | f(x) = x**3 - 4*x**2 + 4*x + 1 f'(x) = 3*x**2 - 8*x + 4 x = 2/3のとき:f'(x) = 0, f(x) = 59/27 x = 2のとき:f'(x) = 0, f(x) = 1 ----------------------------------------------------- | x || -1/3 | ・・・ | 2/3 | ・・・ | 2 | ・・・ | 3 | ----------------------------------------------------- | f'(x) || | + | 0 | - | 0 | + | 0 | ----------------------------------------------------- | f(x) || -22/27 | ↗ | 59/27 | ↘ | 1 | ↗ | 4 | ----------------------------------------------------- |
画像では表が整っているのですが、テキストだとなぜかずれてしまいますね。
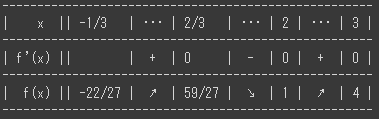
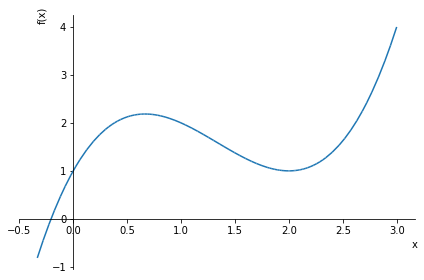
グラフに関しても、必要な部分のみを表示してくれます!
いろいろな関数の増減表を書いてみた
個人的に好きな関数
$$x^{4} – 4x^{2} + 1$$
1 | expr = x**4 - 4*x**2 + 1 |
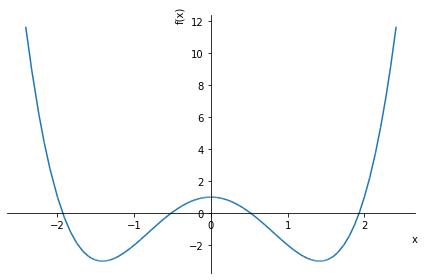

東大受験で用いられてた関数
東大の問題も解いてみましょう。
東大の微分積分の分野は、内容的には難しくはないが、計算量や、計算ミスを誘うような問題が多いと聞いたことがあります。こっちはPCとプログラミングがあるのでチートを使って解いていきます!
関数をプログラムに打ち込むだけなので1分もあれば解けるぜ!
$$f(x) = \frac{x}{x^{2} + 3}$$
1 | expr = x / (x ** 2 + 3) |
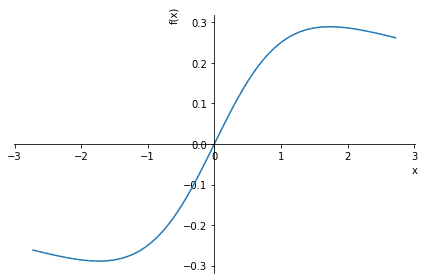

まとめ
今回は、Pythonを用いて、極値を求めて、増減表を作成する方法を記述しました。現状は、三角関数を使った式を求めることはできませんが、指数関数・対数関数などは計算することが出来ます。
増減表を書くためには、たくさんの計算が必要になりますが、この記事にたどり着いた方は式を入れるだけで求まるようになりました。
最後に、極値求める方法を詳しく知りたい方は「Pythonで極値(極大値・極小値)を求める方法【SysPy・argrelmax・argrelmin】」を参考にしてください。
無料の説明会を有効活用しよう!
独学での学習は孤独感を感じやすく挫折してしまう初心者も多いです。また、参考書を購入しても全く読む気にならないという方も多いはずです。
それでも、なんとかPythonの勉強を行い、高スキルなエンジニアを目指したいという方は無料で受けられるオンライン説明会に参加してみることも一つの手です。
Pythonというプログラミング言語は機械学習の人気の高まりなどもあり、様々なスクールが無料説明会を開催しています。
その中でも「Freeks(フリークス)|業界初!10,780円のサブスク型プログラミングスクール」がオススメです。Pythonを効率よく学びたいという方はまずは適性を知るためにも無料説明会を利用しましょう。
 ナノトイラボ
ナノトイラボ 



