ナノトイラボ 
数学の問題を解くときには、関数をグラフ化して考えるとうまくいくことが多いです。今回は、Pythonを用いてグラフを作成していくことで、数学とプログラミングを学んでいきましょう。
特に、高校数学では、グラフを利用して解く問題もあります。グラフの特徴を調べたり、作図するのが面倒になったら、サクッとプログラミングをして、グラフの概形をコンピュータに表示してもらいましょう笑
いろいろな方法でグラフを描画していきますので理解ができると思います。
動作に関しては、「google colaboratory」を用います。環境設定がいらず、無料でGPUを扱えるのでとても便利です。ほかの記事でグラフに関する少し複雑目な内容も記述していますので参考にしてみてください。
関連：Pythonで関数の極大・極小値を求めて増減表を書こう！
関連：PythonでExcelのデータからRGB・HSV色情報の3D散布図を作成
こちらで紹介しているスクールは、すべて無料期間がある優良なスクールのみで、特徴を明確にし、読者のニーズに絞って丁寧に解説しました。初めての一歩として、無料説明会に参加してみてください。
関数とは
数学で言う関数とは、ある変数に依存して決まる一意の値、あるいは、それらの対応を示すものです。 もう少し詳しく説明すると、関数は、数の集合に対しての写像の一種と定義されます。
なので、関数をグラフ化する際には、数と、数に対する値との点を集めた集合がグラフになります。
例えば、下のような関数について考えていきます。
$$f(x) = x (0\leq x \leq1)$$
この関数に、ひたすらに連続する値を代入してみます。
f(0) = 0, f(0.05) = 0.05, f(0.1) = 0.1, …… , f(0.95) = 0.95, f(1) = 1
このような点の集合を一つの表にまとめるとグラフが完成します。
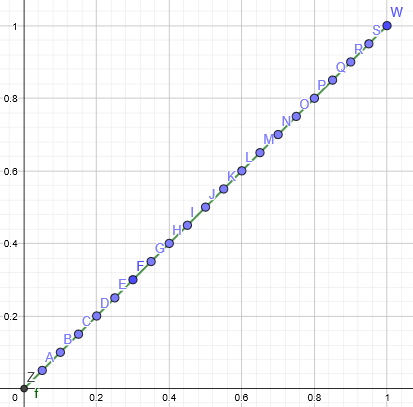
点の集合がグラフになるんだね！
グラフ作成
グラフは点の集合として考える
$$f(x)=x^{3}+3x^{2}+3x+1$$
この関数をグラフ化していきます。
数学で言う関数とは、ある変数に依存して決まる一意の値、あるいは、それらの対応を示すものです。
今回は、「0.1」ずつ変化させてグラフを作成しています。
プログラムを組んで、PCに解かせるからこそできる荒業です。
細かい数字なので、若干の誤差が出てきます。
そのため、「round」関数を用いて少数を丸めています。
詳しい解説が必要な方は下の記事を参考にして下さい。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
import numpy as np import matplotlib.pyplot as plt def f(x): return x**3 + 3 * x**2 + 3 * x + 1 def main(): # f(x)に代入する「x」の値の配列 x = np.arange(-5, 5.1, 0.1) # f(x)の値の配列 y = np.array([f(np.round(i, 1)) for i in x]) plt.title("f(x) = x^3 + 3x^2 + 3x + 1") plt.xlabel("x") plt.ylabel("y") # 補助線をつける plt.grid() x_min, x_max = np.min(x), np.max(x) y_min, y_max = np.min(y), np.max(y) # X軸を設定 plt.hlines(0, x_min, x_max, linestyle='dashed', linewidth = 1) # X軸の下限・上限を設定 plt.xlim(x_min, x_max) # Y軸を設定 plt.vlines(0, y_min, y_max, linestyle='dashed', linewidth = 1) # Y軸の下限・上限を設定 plt.ylim(y_min, y_max) plt.plot(x, y) plt.show() if __name__ == "__main__": main() |
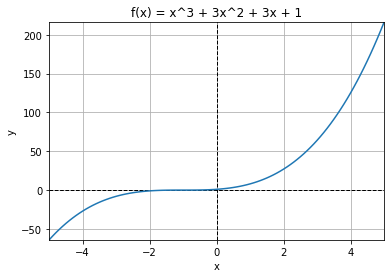
きれいなグラフ！
コードの例は、見た目を整えるための処理が多く、コードが長く見えてしまうかもしれません。しかし、（x, y）座標を取得するためのコードは、9～12行目だけなので、内容は難しくないはずです。
楽にグラフを作成
せっかく「numpy」と「matplotlib」をインポートしているので必殺技を使いましょう。
短く書けることを強調するため、見やすくするための処理は省きます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
import numpy as np import matplotlib.pyplot as plt def main(): # linspace(min, max, N) ： min から max を N 分割 x = np.linspace(-10, 10, 100) y = np.sin(x) plt.plot(x, y) plt.show() if __name__ == "__main__": main() |
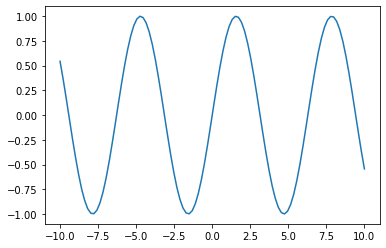
自分で定義した関数を作成
$$f(x) = \begin{cases}-x ^ 3 & (x < 0)\\x ^ 2 & (x \geq 0)\end{cases}$$
このような式をグラフにする方法です。
違いは、最初に「f(x)」で定義するだけなので、最初のパターンとほぼ一緒です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
import numpy as np import matplotlib.pyplot as plt def f(x): if x < 0: return -x ** 3 # ※「else」を使わないほうが無駄な処理を省けるので良い return x ** 2 def main(): x = np.arange(-10, 10.1, 0.1) y = np.array([f(np.round(i, 1)) for i in x]) plt.title("f(x) = (-x^3) if x < 0 else (x ^ 2) ") plt.xlabel("x") plt.ylabel("y") # 補助線をつける plt.grid() x_min, x_max = np.min(x), np.max(x) y_min, y_max = np.min(y), np.max(y) # X軸の下限・上限を設定 plt.xlim(x_min, x_max) # Y軸を設定 plt.vlines(0, y_min, y_max, linestyle='dashed', linewidth = 1) # Y軸の下限・上限を設定 plt.ylim(y_min, y_max) plt.plot(x, y) plt.show() if __name__ == "__main__": main() |
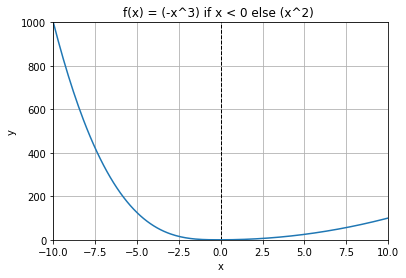
簡単やね！
プログラミングで関数を描画した感想と注意点
数学を勉強したい方は自分で増減表を描いたほうがためになります笑
プログラムに関しては、気に食わない部分があります。
解決できるのかもしれませんが、不連続な関数を与えると、今のままだと意図しない結果になります。
例：f(x) = 1 / x
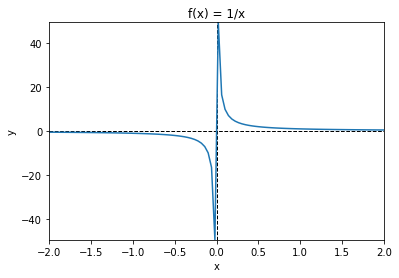
他に面白い関数などは書籍やネットを通してみてみると面白いですね！
まとめ
今回は、数学の関数の概形をプログラミングによって表現する方法を記述しました。
複雑な関数を、グラフにすると、様々な発見があって面白いですよね！
まだ、公開していないのですが、次回は極大値・極小値を求めて増減表を作っていきます！
楽しみにしていてください！
こちらで紹介しているスクールは、すべて無料期間がある優良なスクールのみで、特徴を明確にし、読者のニーズに絞って丁寧に解説しました。初めての一歩として、無料説明会に参加してみてください。
