こんにちわ! このサイトでは回帰分析についてやっていきます。
まず、回帰分析を学んでメリットがあるかという疑問があると思うが
回帰分析を学んでメリットあんの
数字を使って予測することで統計的な、推論に根拠が出る
それにデータがないところについても予測が可能となる
回帰分析を使えば、推測に信憑性がでてくるのだ。
今回は、基本的な概念と回帰モデルについてやっていきます。
導入偏でなので頑張りましょう!
基本的な概念
回帰分析を理解するための例として、ある都市Aの都心部に向かう交通について考えます。
交通需要に影響を与える大きな要素として居住者の人口を挙げる場合、人口が増えるほど交通需要は高まる。
人口が交通需要に影響を与える要因と考え、その影響関係を簡単なイメージにすると下のようになる。
人口 (説明変数) ➡ 将来の交通需要 (目的変数)
交通需要と人口との間の影響関係を分析して予測に使える式を導くことができれば、
容易に将来の需要を推計できる。
回帰分析はこのような影響関係を分析する手法としてしばしば用いられ、導かれる関係式を回帰式と呼ぶ。
人口のように影響を与える側の変数を「説明変数」や「独立変数」と呼ぶ。
交通需要のように影響を受ける側の変数を「目的変数」や「従属変数」,「被説明変数」と呼ぶ。
目的変数は回帰分析において予測の対象となる変数である。
例では、交通需要に与える影響要因として人口のみを取り上げている。
例の場合は説明変数が人口のみなので一つなので単回帰分析という。
実際には、年齢や職業といったさまざまな属性を持った人が、通勤、通学などのあらゆる目的を持って、それぞれに最適と思われる交通手段を利用して移動することが想定される
そのため、交通計画においてA都心部へのトリップ数を予測する際には、居住地域の就業者数、学生数、自家用車の保有台数や、都市地域の企業の営業所数、店舗の延べ床面積など、決定要因となるものが複数考えられる。
このような場合は、説明変数の候補が複数存在することとなり「重回帰分析」と呼ばれる。
回帰モデル式
単回帰分析の例として、都市Aの交通需要について通学トリップの「発生交通量」を15~20歳「人口」から予測することを考える
したがって人口が説明変数、発生交通量が目的変数となる。
都市Aから12のゾーンを選定して人口と発生交通量を調べて結果を表にまとめた。
(表は実際の数値ではなく、計算が楽なように適当につけた)
| ゾーン | 人口(人) | 発生交通量(トリップ) | ゾーン | 人口(人) | 発生交通量(トリップ) | |
| 1 | 2000 | 1500 | 7 | 6000 | 4000 | |
| 2 | 3000 | 2000 | 8 | 5000 | 3500 | |
| 3 | 4000 | 2500 | 9 | 5000 | 3000 | |
| 4 | 5000 | 3000 | 10 | 4000 | 2500 | |
| 5 | 6000 | 3500 | 11 | 3000 | 2000 | |
| 6 | 7000 | 4000 | 12 | 2000 | 1500 |
発生交通量と人口との間に存在する関係を何らかの式で表現できれば、何かできない?
それで将来の発生交通量を人口から予測できるよ
ここで、このデータから散布図を作成すると下の図のようになる。
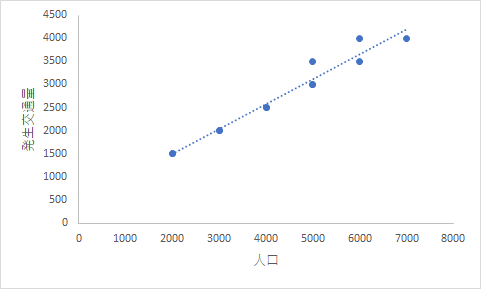
薄い点が回帰直線である。
Excelの機能を使って引かれているものである。
単回帰分析における回帰直線の式(回帰モデル式)は下記に示す
y= a_1 x_1 + b
1 2 3 | <strong>x_1:人口[人] y:発生交通量[トリップ] a_1:係数 b :定数項</strong> |
このように既知データにおける説明変数と目的変数の関係から
最もあてはまりのよい回帰モデル式を導くことができれば
説明変数の新たな値から期待される目的変数(発生交通量)が予測できる。
係数や定数項はモデルパラメータという。
説明変数が二つ以上の重回帰モデルになると、説明変数の数に応じてパラメータも増える
一般にn個の説明変数をもつモデル式は下のようになる
y= a_1 x_1 + a_2 x_2 + ⋯ + a_n x_n + b
1 2 3 4 | <strong>x_1, x_2,⋯ ,x_n:説明変数 y:目的変数 a_1,a_2 ,⋯,a_n:係数 b:定数項 </strong> |
次回に続く
今回は回帰分析の概念と回帰分析についてやりました
次回からモデルパラメータの推定法の最小二乗法についてやっていきます。
 ナノトイラボ
ナノトイラボ 


