Pythonで学ぶ高校数学の美しい物語（フィボナッチ数列と黄金比）

※このサイトの記事内では広告を掲載している場合があります。

私は昔塾で数学を教えていました。

このシリーズの1本目なので取り組みやすいものとして数列を扱います。

コンテンツ

1 フィボナッチ数列とは
2 フィボナッチ数列と黄金比
3 フィボナッチ数列とパスカルの三角形
4 まとめ

無料オンライン相談を活用しよう！

Pythonというプログラミング言語は機械学習の人気の高まりなどもあり、様々なスクールが無料説明会を開催しています。

その中でも「Freeks(フリークス)｜業界初！10,780円のサブスク型プログラミングスクール」がオススメです。Pythonを効率よく学びたいという方はまずは適性を知るためにも無料説明会を利用しましょう。

無料説明会を参加してみる！

フィボナッチ数列とは

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…

という数列です。この数列の特徴は

最初の2項は「1」
第3項目以降は前の2つの項の合計

になっているのが分かると思います。

つまり、フィボナッチ数列の一般項をa_n（a₁ = a₂ = 1）とすると、

a_n = a_{n – 1} ＋ a_{n – 2}

となります。

なので、「89」の次の項は、a₁₂ = a₁₁ + a₁₀ = 89 + 55 = 144となります。

また、第n項を求める一般項は次のように表現できます。

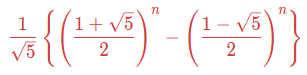
これを「ビネの公式」といいます。

ちなみに、前の3つの項の合計が次の項になる数列を「トリボナッチ数列」といいます。

フィボナッチ数列と黄金比

黄金比とは

黄金比は、φ = (1 + √5) / 2 = 1.618033…と永遠に続く無理数です。

今回の記事では、この値を知っていれば大丈夫です。

ただし、詳しく知りたい方は各自で調べてください。（Wikipedia）

隣り合う2項の比について

a₂/a₁, a₃/a₂, a₄/a₃…のように、a_n+1/a_nを計算していくと、先ほどの黄金比の値に近づいていきます。これは、黄金比の一般項を求める「ビネの公式」と極限を理解していると簡単に説明できます。

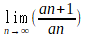
これを計算すると、結局「φ」になります。

黄金比の近似値を求めるプログラム

第n項目と第(n + 1)項目の比を求めるプログラムを作成しました。


import math
import numpy as np
import matplotlib.pyplot as plt

# ビネの公式より
Fibonacci_n  = lambda n : int((((1 + math.sqrt(5)) / 2) ** n - ((1 - math.sqrt(5)) / 2) **n) / math.sqrt(5))
# 第n項目と第(n + 1)項目の比を求める式
calc_ratio = lambda n : Fibonacci_n(n + 1) / Fibonacci_n(n)

# 第1項～第15項まで 
x1 = np.array([i for i in range(1,16)])
y1 = np.array([calc_ratio(i) for i in x1])

# 第15項～第15 * 15 + 1項まで15項ずつ飛ばす
x2 = np.array([i for i in range(15, 15*15 + 1, 15)])
y2 = np.array([calc_ratio(i) for i in x2])

# オブジェクトの生成
fig, ax = plt.subplots()

# y軸の表示範囲の設定（最小値から最大値まで）
ax.set_ylim(np.min(y1) - 0.1, np.max(y1) + 0.1)

# グラフの描写
plt.plot(x1, y1, marker="o", color = "blue", linestyle = "-")

import math

import numpy as np

import matplotlib.pyplot as plt

# ビネの公式より

Fibonacci_n = lambda n : int((((1 + math.sqrt(5)) / 2) ** n - ((1 - math.sqrt(5)) / 2) **n) / math.sqrt(5))

# 第n項目と第(n + 1)項目の比を求める式

calc_ratio = lambda n : Fibonacci_n(n + 1) / Fibonacci_n(n)

# 第1項～第15項まで

x1 = np.array([i for i in range(1,16)])

y1 = np.array([calc_ratio(i) for i in x1])

# 第15項～第15 * 15 + 1項まで15項ずつ飛ばす

x2 = np.array([i for i in range(15, 15*15 + 1, 15)])

y2 = np.array([calc_ratio(i) for i in x2])

# オブジェクトの生成

fig, ax = plt.subplots()

# y軸の表示範囲の設定（最小値から最大値まで）

ax.set_ylim(np.min(y1) - 0.1, np.max(y1) + 0.1)

# グラフの描写

plt.plot(x1, y1, marker="o", color = "blue", linestyle = "-")

グラフの結果は以下の通りです。

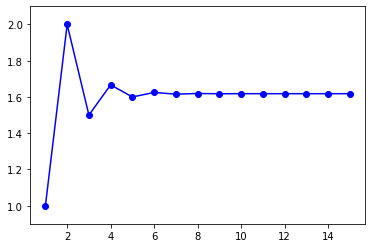
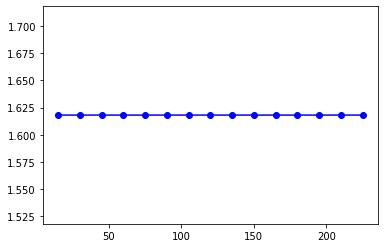
画像の右側の結果を得るためには、サンプルコードの23と26行目の「x1」,「y1」を「x2」,「y2」に変更してください。

試しに以下の命令を実行した時の出力結果は次のようになります。


print(calc_ratio(15 * 15))
# 1.6180339887498947

print(calc_ratio(15 * 15))

# 1.6180339887498947

φ = 1.61803398874989484…なのでかなりの精度で近似値が得られています！すごいですね！

フィボナッチ数列とパスカルの三角形

パスカルの三角形とは

高校数学で二項定理などを習ったと思いますが、そこで扱う係数を並べたものを「パスカルの三角形」といいます。

出典

フィボナッチ数列とパスカルの三角形の関係性

フィボナッチ数列の一般項：a_n = a_{n – 1} ＋ a_{n – 2}

フィボナッチ数列の一般項から、「 a_{n – 1} 」と「 a_{n – 2} 」は次のように変形できます。

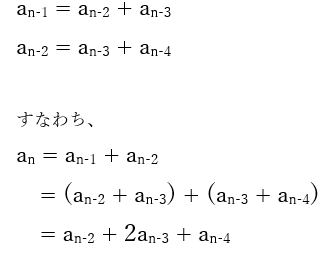
この係数が、先ほどの「パスカルの三角形」と関わってきます。

さらに分解していきます。

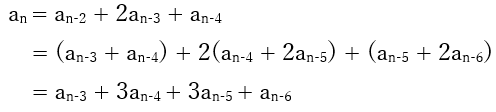
このように、各項を分解していくことで、その係数がパスカルの三角形の数字と一致します。面白いですね！

パスカルの三角形を表現するプログラム

こちらもプログラムを作成してみました。出力結果はきれいな三角形にはならないです。

三角形を表現するためには、桁数を計算して、空白を入れる処理をする必要がありますが、今回はしませんでした。


# 三角形の大きさを設定
N=int(input())
A = []

# 左の「1」を準備
print(1)

for i in range(1, N):
    # 次の段用の配列
    B = [1]

    if i > 1:
        for j in range(1, i):
            B.append(A[j - 1] + A[j])

    # 右の「1」を追加
    B.append(1)
    print(*B)

    # 値のシフト
    A = B

# 三角形の大きさを設定

N=int(input())

A = []

# 左の「1」を準備

print(1)

for i in range(1, N):

# 次の段用の配列

B = [1]

if i > 1:

for j in range(1, i):

B.append(A[j - 1] + A[j])

# 右の「1」を追加

B.append(1)

print(*B)

# 値のシフト

A = B

結果の例は以下の通りです。


"""
10
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
"""

"""

1 1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

1 6 15 20 15 6 1

1 7 21 35 35 21 7 1

1 8 28 56 70 56 28 8 1

1 9 36 84 126 126 84 36 9 1

"""

まとめ

最後までお読みいただきありがとうございます！

今回は、フィボナッチ数列に関わる、「黄金比」と「パスカルの三角形」を表現するプログラムを作成しました。単に手で計算するよりも、プログラムを作成して、大きな数を計算させることによってわかる面白さを感じられたでしょうか！？

今後も数学とPythonで面白いことを公開していくつもりですので、よろしくお願いいたします！

無料の説明会を有効活用しよう！

独学での学習は孤独感を感じやすく挫折してしまう初心者も多いです。また、参考書を購入しても全く読む気にならないという方も多いはずです。

それでも、なんとかPythonの勉強を行い、高スキルなエンジニアを目指したいという方は無料で受けられるオンライン説明会に参加してみることも一つの手です。